RSA TLS AES WTF ?? Partie 2

29 Mar 2020

Key exchange Diffie-Hellmann

Bon déjà le nom est trompeur parce qu'on ne partage pas vraiment les clés telles quelles. On va plutôt échanger des valeurs publiques combinées avec des valeurs privées pour créer une clé commune. Pour bien appréhender la suite, voici l'analogie la plus fréquente. Celle de la peinture, parce qu'une fois mélangée il n'est pas possible de retrouver précisément les teintes d'origine.

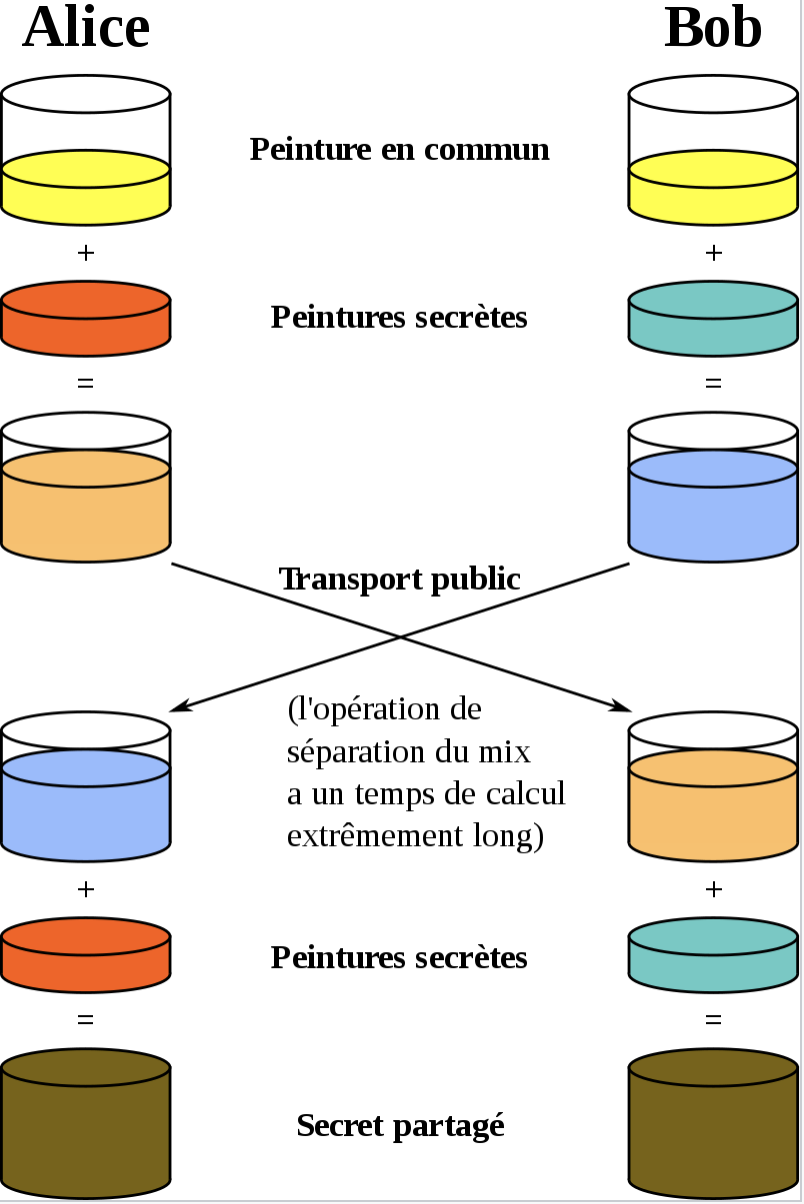
Avant tout, il va falloir que les 2 parties se mettent d'accord sur 2 choses, un "générateur" g et un nombre premier très grand n. Alice possède une clé A privée et Bob une clé B, privée également. Alice et Bob vont utiliser le générateur pour produire une clé publique et privée.

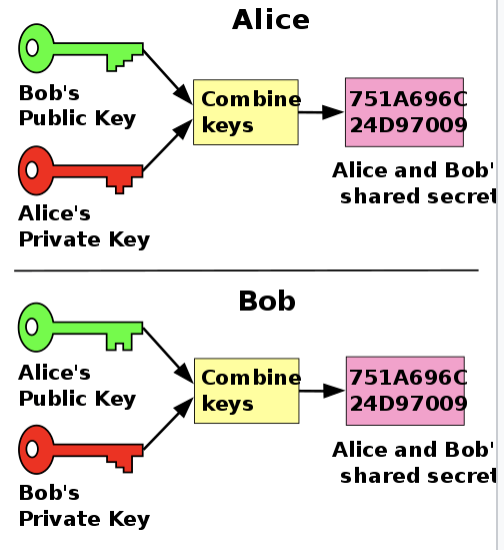
L'idée est qu'une fois les 2 utilisée, il doit être impossible de faire machine arrière et retrouver les valeurs initiales. On obtient donc Ag et Bg. Ces deux valeurs sont échangées publiquement. Un attaquant possède donc Ag, Bg, g. mais ni A ni B. Alice va ajouter A, à Bg, et Bob va ajouter B à Ag. On va obtenir des 2 côtés une clé conçu depuis A, B et g. Sans les clés privés on peux obtenir éventuellement ABgg mais pas ABg.

En 3 passes, on a maintenant une clé privée que seuls les 2 interlocuteurs connaissent. On va vouloir faire ça au début de chaque "échange".

Pour sécuriser le tout encore plus, dans les méthodes modernes que l'on utilise, on va également y ajouter des données variables pour in fine obtenir un nombre qui sera haché pour être utilisé comme clé secrète dans les algorithmes de chiffrage comme AES.

Maintenant que le principe est connu, allons couvrir les maths. Dans le domaine public il y a g et n. g est un nombre premier, souvent petit. n est un grand nombre premier. Souvent autour de 2000bits, mais de plus en plus autour de 4000bits. Alors grand oui mais il ne peut pas être trop grand, sinon on perd en rapidité de calcul ce quel l'on a gagné en sécurité, il faut un juste milieu, d'ou l'importance du choix de n, même si techniquement, on peut trouver la valeur, ça prendrait tellement de temps qu'on a aucun intérêt ne serait-ce que d'essayer.

Alice choisi une valeur A entre 1 et n, souvent un grand nombre aléatoire, que l'on ne partage pas. Bob choisi une valeur B de la même manière.

Alice calcule \(Ak = g^A mod n\). modulo c'est le restant de la division. Si on devait le rendre visuel, modulo est un cercle de valeur et nous allons faire autant de tours que possible avant d'arriver à la valeur désirée. Donc on va élever une valeur à la puissance d'une seconde valeur monstrueusement grande, mais au final avec modulo on va restreindre le résultat dans l'espace qu'autorise n. Ce qu'il faut noter c'est que selon les facteurs initiaux il y a plusieurs possibilités d'obtenir le même résultat, ce qui rends très difficile la possibilité de retrouver la valeur de A. Le seul moyen ce serait de brute-forcer les résultats et vous n'êtes pas couchés.

Bob va calculer \(Bk = g^B mod n\) 

Ces 2 valeurs sont partagées publiquement.

Alice va exécuter à nouveau le calcul mais avec la clé de bob 

\(Bk^A mod n\)

et Bob exécutera \(Ak^B mod n\)

Ce qui donnera le même résultat. Ils ont donc la même clé privée en leur possession, pour chiffrer leurs échanges.

La limite de l'échange

La problématique de l'échange de clés c'est qu'il faut avoir confiance dans votre réseau internet.

Si quelqu'un a la maitrise du réseau, il se positionne en tant qu'intermédiaire. Lorsque votre navigateur soumet les requêtes d'échanges de clés, l'attaquant peut intercepter le message, générer une clé privée et soumettre la clé publique à votre navigateur. D'un point de vue réseau aucune raison de douter qu'il ne puisse pas s'agir du serveur visé initialement. Il va ensuite demander au serveur visé d'établir un échange de clés à la place de votre navigateur. Il est maintenant capable de décoder vos messages et en faire ce qu'il veux avant de les envoyer au serveur et de vous renvoyer la réponse (en prenant soin soit d'enregistrer la réponse voire même de la modifier à votre insu).

C'est un gros problème parce que Diffie-Hellmann ne permet pas de prévenir ce genre d'attaque et que votre téléphone essaie systématiquement de se connecter à un réseau public connu ou un réseau privé déjà enregistré. il est assez facile via des outils comme shodan.io de détecter le matériel utilisé et de tenter les accès par défaut du-dit router… Méfiez-vous des réseaux publics.

C'est là que RSA entre en jeu.

Puisque qu'il n'est possible de décoder un message chiffré avec la clé privée uniquement avec la clé publique associée, le serveur va utiliser la clé privée pour chiffrer le résultat du nombre premier passé dans le générateur. Si je suis capable de déchiffrer, je suis donc certain que le message provient bien du serveur visé. Si on considère bien sûr que la clé privée n'ait pas été rendue publique par erreur.

Il y a toujours un risque bien, sûr alors il existe plusieurs variations de cet algorithme. Dans certains les clés sont renouvelées de manière régulière.

Pour y ajouter encore en complexité, il est possible de retrouver également des mécanismes ou l'on signe le message, pour cela on va générer un hash.

Hashing

Tout le monde connais SHA 1 - secure hashing algorithm

Ce qui est amusant puisqu'il n'est plus assez "secure". 

Des recherches ont démontré des failles dans l'algorithme, dès 2005.

Mais pas de souci, car avec les technologies de l'époque, il fallait injecter l'équivalent de 2,7milliard€ en matériel. C'était donc une attaque théorique.

En 2015 les cartes graphiques progressent et on rentre dans le domaine du possible. avec 64GPU en cluster on arrive à provoquer des collisions et commencer à décoder tout ou parties d'un message. Il faut donc estimer autour de 120k € pour une attaque. Autant dire que pour un état ou des criminels bien établis c'est de la petite monnaie.

En 2017 c'est fini. Une technique particulière met un K.O. a SHA1, il faut se tourner vers SHA2 ou AES.

Pour comprendre la technique, il faut d'abord comprendre SHA. C'est un algorithme qui transforme n'importe quelle chaine en une chaine de 160bits. Pour fonctionner SHA à besoin en entrée d'une chaine de 512bits et utilise une fonction de compression qui prendra des groupes de bits pour n'en rendre qu'un seul. Si la chaine est supérieure à 512bits on découpera en blocks de 512. Et puisqu'une chaine ne fait jamais 512bits, il faut un moyen de la rallonger. on va ajouter un bit positif, puis des 0 et terminer par la longueur du message. s'il fait 7 de long on rajoute 111 à la fin donc 1010111 100000…000111. la fonction de compression va effectuer des décalage de bits à partir d'une matrice définie dans l'implémentation. L'algorithme exécutera 80 fois la fonction de compression. Pour obtenir une chaine de 160bits.

Puisque la matrice est définie, on obtiendra toujours les mêmes résultats pour la même chaine. Problème il y a donc une faible possibilité que différents inputs puissent produire le même hash. 

La technique utilisée pour l'attaque permet de réduire le nombre de variations à tester pour y arriver.

Cette technique c'est le paradox des bébés ! Ou birthday paradox ou Birthday-near-collision attack. Avec cette approche, on va beaucoup, beaucoup plus vite qu'avec les précédentes techniques. Je vous explique le principe.


Parmi 23 bébés né en 2019 dans le monde.
Quelle est la probabilité pour ces bébés d'avoir la même date de naissance? \(23\over365\) soit 6%, pas du tout. C'est 50%. Et si on pousse jusqu'a 50 bébés on arrive à 97% de chance. À 75 on touche les 99.97%. C'est un paradox, il semble absurde mais on a les maths pour le prouver. Comment est-ce possible qu'un si petit nombre ai autant de chance d'avoir le même anniversaire ? Comment prouver parmi les 365 possibilités, qu'un sixième suffise ? En fait, on va plutôt prouver le contraire, on va prouver qu'ils n'ont pas, le même anniversaire. C'est plus facile.

Le bébé 1 est né. il a donc la totalité des choix possible \(365\over365\).

Le bébé 2 est né. la probabilité qu'il n'ai pas le même anniversaire est \({365\over365} \times {364\over365}\). Un jour de moins que le nombre de bébés déjà nés.

Le bébé 3 est né \({365 \over 365} \times {364\over365} \times {363\over365}\)

Le bébé 4 est né \({365 \over 365} \times {364\over365} \times {363\over365} \times {362\over365}\)

Etc...

Ce calcul a une expression plus simple, on dit que c'est factoriel de 364 divisé par factoriel de 365 -le nombre de bébés * 365 (le nombre de jours dans l'année) à la puissance du nombre de bébé -1

Pour 23 bébés, nous attendons donc le résultat de \(364!\over(342!\times365^{22})\)

Ce qui nous donne, 0.492703 soit approximativement 49.3% de chance que ces bébés n'aient pas la même date de naissance.

Le truc ici c'est qu'on évalue la probabilité de chacun des bébés entre-eux.

On ne vérifie pas qu'un des bébés de 2 à 23 possède le même anniversaire que bébé 1 parmi les 365 possibilités, mais plutôt que 2 bébés parmi les 23 puisse posséder le même anniversaire au sein des 365 possibilités. C'est surprenant mais les Maths le prouvent. Et très logiquement, plus on ajoute de bébés, plus on augmente ce risque d'interpolation.

C'est la même idée qui va être appliquée pour provoquer des collisions, ce qu'essaient de faire les chercheurs.

En admettant que j'ai un fichier en ma possession produisant le hash : \(99024280cab824efca53a5d1341b9210\)
Je vais tenter de produire une autre chaine qui possède le meme hash.
Pour le faire je vais créer une multitude de caractères, espaces, virgules, nouvelles lignes, apostrophes, etc. En créer un nombre conséquent de variations je vais finir éventuellement par tomber sur le même hash (c'est une collision). Ainsi, lorsque je vais demander à mon client de signer de manière électronique mon "vrai" document, je vais ensuite en profiter pour attacher la signature au "faux" document. Ce qui sera valide puisqu'ils produisent le même hash. (pour se protéger créer une copie chez vous du document juste après avoir signé).

Plutôt que de tenter de trouver la possibilité qu'une valeur soit une autre, ce qui représente \(3.4\times10^{38}\) possibilités à vérifier et donc de variation à produire, on a pris le problème à l'envers en utilisant un algorithme basé sur le birthday paradox afin de réduire les possibilités et provoquer des collisions avec moins d'essais possibles.

MD5 et SHA1 sont cassés.

Alors attention prenons des pincettes tous de même, il n'y a aucune urgence.

SHA1 produit un résultat de 160bits, ayant une probabilité de collision de \(1^{280}\), soit environ 12millions d'années de calcul GPU, tellement long que même la NSA, n'essaiera même pas. Avec la méthode ci-dessus, on abaisse cette probabilité à \(2^{60}\) ce qui devient possible, avec beaucoup d'argent et une grande puissance de calcul. Malgré tous il n'y a aucune raison de ne pas passer à SHA2 puisqu'on passe de 160 à 256 et 512 bits. On arrive donc à une probabilité de \(2^{128}\), ce qui est considérablement plus grand. Mais le fait que ce soit possible, reste un risque.

Alors on imagine d'autres moyen de hasher nos données et de rendre encore plus "aléatoire" le résultat. Les algorithmes modernes utilisent un SPNetwork.

SP Network

A suivre...